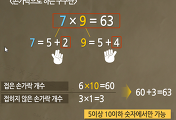
곱셈과 나눗셈
4-1-2 단원 - 초등학교 곱셈 연산의 최종 마무리 단계. 보완할 기회 없음.
수포자 학생 발생의 결정적 단원. 3학년에서 나눗셈 기초에서 한 번 어려움을 겪은 바 있다.
표준 곱셈 알고리즘 완벽한 이해 필요. 나눗셈의 기본 알고리즘도 완결하도록 되어 있다. 전체 단원 중 가장 많은 시간이 배당됨. 익숙해지도록 완벽하게 하고 넘어가야 한다. 아니면 이후의 학습이 어려워짐
1) 만의 열 배 는 10만이다 = 10000 X 10 = 100000 '배'=X 로 나타냄을 지도.
2) 십진법 표기의 곱하기 표시
ⓐ12X3000 과 ⓑ200X3000 어느 것이 더 쉬운가? 자릿수는 ⓐ가 작지만 셈은 ⓑ가 더 쉽다. 지릿수 조정만 하면 됨.
곱셈 단원의 활동 여러 가지는 아래의 2단계로 구성된다. (1)~(4)는 십진법 안에서 0의 역할과 자릿수 개념정립 문제
(5),(6)이 본격적인 곱셈임.
3) 곱셈에 필요한 자릿수 개념
아이들이 0을 세어서만 구했는지 십진법 개념을 알고 구했는지 알아봐야 함.
기계적인 아이는 셈의 형태만 달라져도 구하지 못하는 경우가 생김 (가로셈-세로셈)
선행학습에 의한 절차적 지식만을 가진 아이, 어찌 파악하나?
큰 수에서 배웠던 것을 응용. -> 323000 = 3X100000 + 2X10000 + 3X1000 이듯이.
연산기호를 사용하여 큰 수를 나타내는 연습을 하자. 자릿수를 이해할 수 잇음.
4) 연산에서의 어림
세자리수 X 두자리수의 연산
초등수학에서 어림셈은 필요? - 매우 중요, 지금은 아니다. 집중 교수 내용은 곱셈 알고리즘이다.
<학생들이 힘겨워 할 절차>
* 자릿값에 집중하여 신경 써야 함
* 0의 역할 인지
* 분배법칙을 직관적으로 활용 (피승수 X 10의자리 + 피승수 X 일의 자리)
→ 어림셈 병행보다 곱셈 알고리즘 이해에 초점을 두자
곱셈의 원리를 체득하는 데 중점을 둔 수업은 무엇인가?
* 분배법칙을 직관적으로 활용 (피승수 X 10의자리 + 피승수 X 일의 자리)
[대안찾기]
1) X100, X1000, X10000등등은 큰 수 단원에서 십진법 개념지도와 병행한다.
2) 3학년 수준의 두자리수X두자리수 문제를 제시하여 곱셈 알고리즘을 충분히 알고 있는지 측정, 정답률에 따라 진도와 복습을 결정한다.
: 정답을 얻기까지의 풀이 과정을 설명해 보도록 제시
풀이 과정에 대해 답변하지 못한다면 "왜 그렇게 생각합니까?" 의 질문 필요
3) 곱셈 알고리즘 점검하기
 |  |  |
당연하게 생각하는 것에 대한의문을 유도하자.
4) 곱셈 알고리즘의 분배법칙
일본의 경우,
5) 세로셈에서의 자릿값
* 알고리즘 다지기
'생각, 공부 > 연수 기록' 카테고리의 다른 글
| 수학 르네상스-분수 (단위분수의 위력) (0) | 2015.03.18 |
|---|---|
| 수학 르네상스 - 곱셈의 다른 방법 (0) | 2015.03.17 |
| STEAM과 세계 (0) | 2014.04.22 |
| STEAM 과 미래 (0) | 2014.04.22 |
| STEAM 교육을 위한 다양한 참고 자료 (0) | 2014.04.22 |